Pass by Reference
Pass by reference popularly described as passing by address, is a system of passing reference of statement in a call function to simultaneously correspond with the standard parameter of the called function hence a copy of the address of the standard parameter is registered in memory, making it possible and mandating it that both the caller and the callee utilize and operate on the same variable for a parameter. Pass by Reference (Pass by Address), simply has to do with storing a copy of the address of the real existing parameter. Often employed when when changing the parameter passed in by the client program to make it different in some way.
The good thing about passing objects by reference is that it enhances the ability to effectively maximize the use of memory and minimize time consumption in processing data. The only downside to passing an object by reference is that the function will be able to change the original object that was passed to it.
The Process Involved in Call by Reference
The process involved essentially has to do with both caller and callee’s request referencing the same locations in that any modifications effected on the stored function on the memory for processing both caller and callee’s requests are reflected on both. Whenever a call is passed, it would be directed to the statement corresponding to the function (referencing) and then copied to the formal parameter of the callee which is then utilized for processing the request in the statement of the call passed.
The process requires the programmer to declare the parameters in the function that would be set as the reference hence, the operation function can be related to a swap() since it has to do with the exchange of values into the corresponding variables.
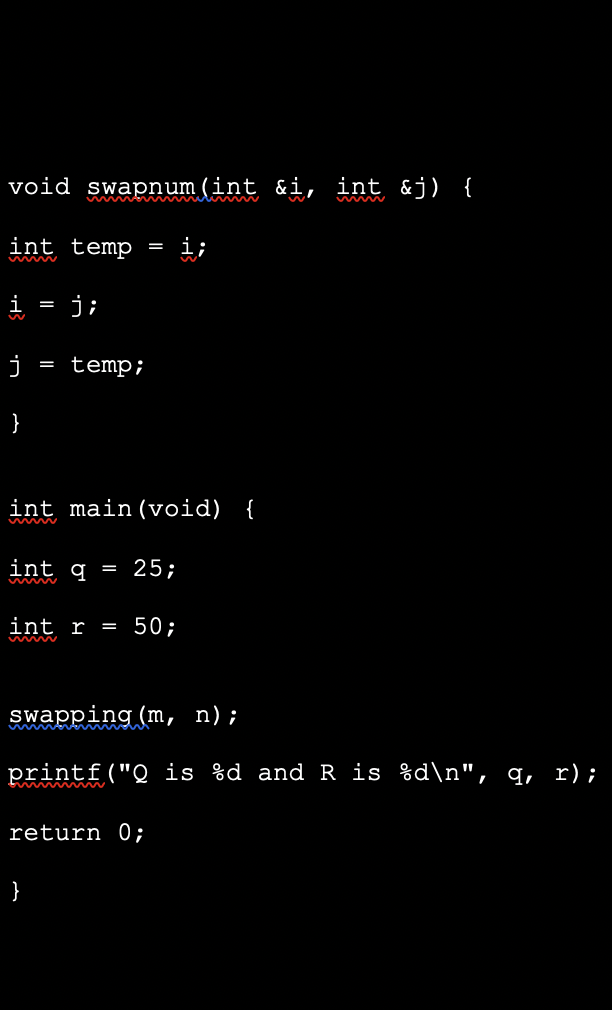
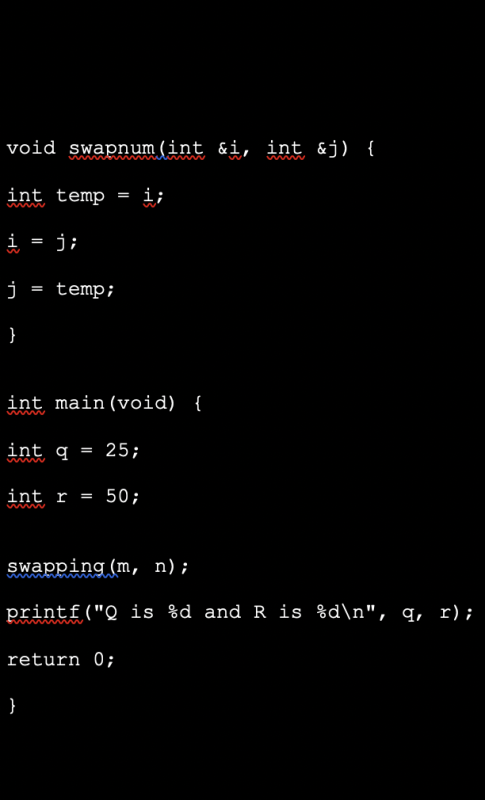
Example on c++
#include
void swapnum(int &i, int &j) {
int temp = i;
i = j;
j = temp;
}
int main(void) {
int q = 25;
int r = 50;
swapping(m, n);
printf("Q is %d and R is %d\n", q, r);
return 0;
}
Whenever swapnum() is called, triggers the exchange of the variable values q and r since it is a pass by reference. Hence output is:
Q is 50 and R is 25
Advantage of Pass by Reference
Call by reference becomes very advantageous as its usefulness becomes obvious where a function is required to interchange the value of the statement of a request without duplicating data for retaining a value hence maximizing memory space as it does not store a copy of the request made in this method, The whole algorithm supports swift processing of data making very fast, does not allow for modification of the function by an error by the reader of the code.
Disadvantage Pass by Reference
It does not store the statement and output of the request, loss of data is inevitable since it output of a process parameter is not stored though the user can copy and save the outputs it is not automatically stored, hence the copy of the variable changes and not the original.
Recursive approaches can be employed in sorting algorithms, making sorting of n variables in O(nlogn) time likened to O(n^2) efficiency of a sortation.
Sorting is a way of ranking or organizing data that has a specific list of order that enables a series of consistent splitting of the list into divisions mainly two and passing both the ascending and descending arrays to different sides. there are different types of sorting which include bubbleSort, insertionSort, selectionSort, bucketSort, heapSort, quickSort, and so on; of all the sortation methods, recursion is more predominantly important in quickSort and mergeSort. Sorting using quickSort, for instance, takes the higher array of data to one side and the lesser array to the other. It begins by taking one item from the whole list to be a pivot point; it, therefore, derived its name Quicksort from its traits of efficiency with the fastest run time standard in the history of the memory sorting algorithm for an average case.
Recursion can be implemented using a sorting algorithm that has a worst-case running time as O(n^2) this is from an input array of n numbers. Even in slow worst-case run time. Sorting is a widespread and well-sought-after technique that provides a real solution, and credible standardized efficiency, in addition, to ease of implementation while supporting various types of input data with speeds that operate on different methods of sorting. The running time algorithm is popularly represented by n log n notation for sorting n number of items with a very short inner recursion.
Example Using quickSort as a Case Study
In the array {55, 44, 73, 11, 15, 7, 3, 19}, we would select the random number 19 as the pivot. Therefore, following the first pass, the list changes to something like this: {3, 9, 11, 15, 44, 55, 73}, looking at the arrays in this example, we would notice that the pivot number 15 is standing right at the middle, hence sharing the items into two where the values lower than the pivot are ordered to the left and the ones higher, are set to the right however, the same decremental iteration process applies to both sides until it decreases to the very least that can be processed, pivot does not necessarily have to be in the middle.
On the running time of sorting, (n) reiteration times for the recursion such that each stage of the abstraction maintains n value until a final limit has been reached at O(n log n) = O(n^2, where the levels maintain the highest cost as n). When the recursion of a task ends at a point where its proportional to the number of reiterations without conscious reasoning becomes unbalanced, sortation executes in the recursion process in O(n log n) execution time till it reaches the least value, because any division of a constant proportionality would produce a reiteration tree of depth O(log n), with n at every level being O(n). The execution time would hence be O(n log n) anytime the division has constant proportionality hence recursion of the algorithm makes it more asymptotically efficient in terms of processing and time management. Big O notation is generally used to refer to the upper bound, putting aside the reduction of i, one can analyze the order of an algorithm as n * n i.e n^2 or O(n^2) recursion.
The upper bound and lower bounds of the algorithm are used to identify algorithms behaviors, the upper bound is for detecting the progress/increase in the algorithm’s running time pointing to the upper or highest growth frequency an algorithm can have i.e. the recursion rate; the lower bound uses notation to describe the smallest amount of a supply that an algorithm requires for some class of input, corresponding to the big-Oh notation, is a measure of the algorithm’s increasing rate. Nonetheless, if in O(n), n has a fixed value or swap file of say 1, then the algorithm is said to be constant time and of fixed duration, because it does not modify the order of increment/size; say in a substantially high swap file and instruction included to ignore it when values are already in sorted order, then the substantial time may be stored hence, a single iteration of i values with j running from 0 … i–1 undertaking only a contrast- not a swap to each is adequate to validate the values are sorted.
Conclusion
Recursive thinking is really important in programming. It helps you break down bit problems into smaller ones. Often, the recursive solution is most importantly used in Quick sort and merge sort as a crucial technique making a function recursively call on itself, directly or indirectly, until a specified condition has been reached i.e. where it hits the stopping point as defined in the function hence solving time complexities in processing and helping the program process tasks seamlessly.
When the function swapnum() is called, the values of the variables x and y are swapped since both are passed by reference.